四级编程题训练
抽奖程序
在编写抽奖程序时,为了保证一个人只有一次中奖机会,要检查新抽出来的数字是不是已经被抽中过了。
一种办法是将已经中过奖的人员编号存放在test_list里面,然后每抽出一个新的人员编号,判断它是否在中奖人员列表中。
如果没有在中奖人员列表中,说明中奖号码有效,并将它保存进中奖人员列表;如果已经在里面了,就再生成一个新的人员编号。
请你补全下面的代码,实现判断一个数字是否在列表中的功能。
#子问题算法(子问题规模为1)
def is_in_list(init_list,num):
if init_list[0] == num:
return True
else:
return False
#分治法
def find_out(init_list,num):
n = len(init_list)
if ____①______ #如果问题的规模等于1,直接解决
return is_in_list(init_list,num)
#分解(子问题规模为n/2)
left_list,right_list = _________②____________
#递归,分治,合并
res=find_out(left_list,num) __③__ find_out(right_list,num)
return res
if __name__ == "__main__":
#测试数据
test_list = [18,43,21,3,28,2,46,25,32,40,14,36]
#查找
print(_____④_____)
程序运行结果:
>>>True
参考答案:
(1) n==1: 或其他正确答案; (2分)
(2) init_list[:n//2], init_list[n//2:] 或其他正确答案; (2分)
(3) or 或其他正确答案; (2分)
(4) find_out(test_list,25) 或其他正确答案。 (2分)
乘法运算
乘法运算等于多个加法运算的和。比如,3×2可以理解为3+3,也可以理解为2+2+2 。
下面的程序使用递归算法演示了计算两个自然数的乘积的过程。请你补全代码。
输入:分两次输入自然数num1,num2
输出:num1 × num2 = 乘积
def cheng_fa(num1,num2,value):
if _____①_____
value += 0
else:
value += num1
_____②_____
value = cheng_fa(num1,num2,value)
return ____③ _____
num1=int(input('输入第1个数:'))
num2=int(input('输入第2个数:'))
value=0
value = cheng_fa(num1,num2,value)
print('{} X {} = {}'.format(num1,num2,value))
程序运行结果:
输入第1个数:3
输入第2个数:7
3 X 7 = 21
参考答案:
(1)num1==0 or num2==0: 或其他等效答案 ;(3分)
(2)num2 -= 1 或 num2=num2 - 1 或其他等效答案; (4分)
(3)value 。(3分)
计算骑行时间
外卖送餐服务越来越受到人们的喜爱,外卖小哥们也成了路上的一道风景。
当顾客使用外卖软件点餐时,会出现一个预计送达时间,包括了餐厅制作食物的时间,路上的骑行时间等等。
一种常用的计算路上骑行时间的方法是用曼哈顿距离(manhatton distance)除以平均骑行速度。平面上点A(x1,y1)与点B(x2,y2)的曼哈顿距离为:|x1-x2|+|y1-y2|。
假设一名外卖小哥的平均骑行速度为30km/h。下面的程序模拟计算外卖小哥的路上骑行时间,请你补充完整。
输入:分两次输入A点和B点的坐标值
输出:A、B两点间的曼哈顿距离和路上骑行时间。
#求绝对值
def my_abs(n):
if _____①_____
return n
else:
return _____②_____
#主程序
v=30 #平均骑行速度
x1=float(input('输入A点的x坐标(米):'))
y1=float(input('输入A点的y坐标(米):'))
x2=float(input('输入B点的x坐标(米):'))
y2=float(input('输入B点的y坐标(米):'))
#计算曼哈顿距离mht
mht = _____③_____
#计算路上骑行时间
time_on_the_road = _____④ _____
print('A、B两点的曼哈顿距离为{}米'.format(mht))
print('预计路上骑行时间需要{}分钟'.format(time_on_the_road))
程序运行结果:
输入A点的x坐标(米):-1000
输入A点的y坐标(米):1000
输入B点的x坐标(米):1000
输入B点的y坐标(米):-1000
A、B两点的曼哈顿距离为4000米
预计路上骑行时间需要8.0分钟
参考答案:
(1) n>0: 或 n>=0: (2分)
(2) -n (2分)
(3)my_abs(x1-x2)+my_abs(y1-y2) 或 sum([my_abs(x1-x2),my_abs(y1-y2)]) 或 sum((my_abs(x1-x2),my_abs(y1-y2))) 或其他等效答案; (4分)
(4)mht/1000/v60 或 mht/(1000v)60 或 mht60/1000/v 或 (mht60)/(1000v)或其他等效答案 。(4分)
质数判断
质数是一个大于1的自然数,除了1和它本身外,不能被其他自然数整除。下面的程序设计中,先自定义一个函数,用来判断一个数是否为质数。然后,通过键盘输入一个数,调用所编写的函数,判断该输入的数是否为质数。请根据上述设计思想,完成程序段中划线处的填空。
def findprime(m):
for i in range(2,m):
if _______① _____:
return False
return ________ ② _____
n = int(input('请输入一个数:'))
if _______③ _____:
print("该数是质数.")
else:
print("该数不是质数.")
参考答案:
① m % i ==0 (3分)
② True (3分)
③ findprime(n) (4分)
二分法查找
随机生成的10个在[1,100)范围内整数存入列表;输入一个待查找的整数k,运用二分法在列表中查找k,根据查找状态输出对应的结果,请将程序补充完整。
from random import randint
def b(s,v):
top=0
last=len(s)
while _____① ______
mid=(top+last)//2
if v==s[mid]:
return mid
elif v>s[mid]:
_____② ______
elif v<s[mid]:
last=mid-1
return None
s=[randint(1,100) for i in range(10)]
s.sort()
print(s)
k=int(input())
ans=b(s,k)
if _____③ ______
print('找到,下标是:',ans)
else:
print('没有找到这个数!')
运行结果1:
[13, 25, 27, 41, 52, 66, 67, 69, 72, 75]
72
找到,下标是: 8
运行结果2:
[9, 15, 16, 19, 27, 31, 43, 64, 84, 93]
20
没有找到这个数
参考答案:
①top<=last:或等效答案;(2分)
②top=mid+1或等效答案;(3分)
③ans!=None: 或等效答案;(3分)
兔子数量问题
有一群兔子,4个4个地数余1个,5个5个地数余2个,9个9个地数余7个,试问兔子有多少只?(请将程序补充完整)
def _____① _____
while _____② _____
if n%5==2:
break
n+=9
while True:
if _____③ _____
break
n+=45
print(n)
f(16)
参考答案:
① f(n):或等效答案;(4分)
② True:或等效答案;(4分)
③ n%4==1:或等效答案;(4分)
分治思想计算最大值
利用分治思想,给定一个顺序表,编写一个求出其最大值的程序。
根据上述算法思想,补全下列代码。
输入输出示例:当顺序表是 [22,13,34,4,68,15,5,58,36],输出:68
def fun_max(num=list):
return max(num)
def fun(num):
n = _____①_____
if n <= 2:
return _____②_____
l_list, r_list = num[:n//2], num[n//2:]
l_max, r_max = _____③_____
return fun_max( _____④_____)
if __name__ == "__main__":
alist = [22,13,34,4,68,15,5,58,36]
print(fun(alist))
参考答案:
① len(num) 或等效答案; (2分)
② fun_max(num) 或等效答案; (2分)
③ fun(l_list), fun(r_list) 或等效答案; (2分)
④ [l_max, r_max] 或等效答案;(2分)
出局游戏
现有n个人依次围成一圈玩游戏,从第1个人开始报数,数到第m个人出局,然后从出局的下一个人开始报数,数到第m个人又出局,...,如此反复到只剩下最后一个是胜利者。设n个人的编号分别为1,2,...,n,打印出局的顺序。
根据上述算法思想,补全下列代码。
输入输出示例:当n=10,m=4,输出如下:
出局的人是: 4
出局的人是: 8
出局的人是: 2
出局的人是: 7
出局的人是: 3
出局的人是: 10
出局的人是: 9
出局的人是: 1
出局的人是: 6
最后胜利者是: 5
def fun(n,k):
L = list(_____①_____)
if n == 1:
return
else:
x = 0
for i in _____②_____
x = _____③_____ - 1
print('出局的人是:',L[x])
del L[x]
if x < 0:
x = 0
print('最后胜利者是:', _____④_____)
fun(10,4)
参考程序:
① range(1,n+1) 或等效答案;(3分) ② range(n-1): 或等效答案;(3分) ③ (x + k) % len(L) 或等效答案;(3分) ④ L[0] 或等效答案;(3分)
分解质因数
设计一个算法,将一个正整数分解质因数。
程序分析:对n进行分解质因数,应先找到一个最小的质数k,然后按下述步骤完成:
(1)如果这个质数恰等于n,则说明分解质因数的过程已经结束,输出即可。
(2)如果n>k,但n能被k整除,则应打印出k的值,并用n除以k的商,作为新的正整数n,重复执行第一步。
(3)如果n不能被k整除,则用k+1作为k的值,重复执行第一步。
根据上述算法思想,补全下列代码。
输入输出示例:
当n=105,输出:105= 3*5*7
当n=60,输出:60= 2*2*3*5
def fun(n):
print('%d='%n,end=' ')
for i in _____①_____:
while n!=i:
if n>i and _____②_____ :
print(i,end='*')
_____③_____
else:
break
else:
_____④_____
break
if __name__ == "__main__":
while True:
num=input("输入一个正整数:")
if not num.isdigit():
break
fun(int(num))
参考答案:
① range(2,n+1) 或等效答案;(3分)
② n%i==0 或等效答案;(3分)
③ n=n//i 或等效答案;(2分)
④ print(n) 或等效答案;(2分)
回文数
要求:设计一个算法,如果一个数从左边读和从右边读都是同一个数,就称为回文数。例如9889就是一个回文数,求对于用户输入的一个非零正整数判断是否为回文数。
根据上述算法思想,补全下列代码。 示例:输入9889,返回9889是回文数;输入34542,返回34542不是回文数。
i=input("请输入一个非零正整数:")
n=len(i)
if _____①_____:
for j in range(int((n+1)/2)):
if _____② _____:
if n==2*j+1:
print("{}是回文数".format(i))
else:
print("{}不是回文数".format(i))
break
else:
for j in _____③_____:
if i[j]==i[n-j-1]:
if _____④_____:
print("{}是回文数".format(i))
else:
print("{}不是回文数".format(i))
break
参考答案:
① n%2!=0: 或等效答案;(3分) ② i[j]==i[n-j-1]: 或等效答案;(3分) ③ range(int(n/2)) 或等效答案;(2分) ④ n==2*(j+1) 或等效答案;(2分)
成绩查询
任务:利用分治思想,在50个同学成绩(成绩不重复)中查找指定成绩的同学的编号,学生成绩存储在列表cj中;待查找的成绩由键盘输入到变量key中。根据上述算法思想,编写自定义函数完成程序功能,完善空白处代码。
"""
函数名def search(lft,rgt,key)
参数表:整数lft,rgt表示待查找列表的左右边界,key是待查找的成绩
返回值:找到返回key所在编号,否则返回-1.
"""
def search(lft,rgt,key):
if lft>rgt:
return -1
mid = _____①_____
if cj[mid] == key:
return mid
elif _____②_____ :
lft = mid + 1
else:
rgt = mid - 1
_____③_____
import random
cj = [random.randint(1,100) for i in range(50)]
cj.sort()
key = int(input("输入待查找的成绩"))
pos = search(0,49,key)
print(pos)
参考答案:
① (lft+rgt)//2 (2分) ② cj[mid] < key (3分) ③ return search(lft,rgt,key) (3分)
最大公约数
要求:设计一个算法,对于给定两个正整数,求它们的最大公约数。
根据上述算法思想,补全下列代码。
函数名:gcd(x,y) 参数表:x-- 整数x,y-- 整数y。 返回值:它们的最大公约数。 示例:当x=6,y=9时,返回3。
def gcd(x,y):
if _____①_____:
return y
else:
return _____②_____
sums = 0
m = int(input('请输入第一个正整数m = '))
n = int(input('请输入第二个正整数n = '))
sums= _____③_____
print("m和n两个正整数的最大公约数是:%d"% sums)
参考答案:
① x%y== 0或等效答案;(4分) ② gcd(y,x%y) 或等效答案;(4分) ③ gcd(m,n) 或等效答案;(4分)
评委打分
7个评委给每个选手打分,评委分数中去掉最高分与最低分,计算所得平均分是每个选手的最后得分,保留2位小数。
根据上述计算规则,编写自定义函数完成程序功能,完善代码。
"""
根据评委分数,计算去掉最高分与最低分后的平均分,保留2位小数
函数名 def getScore(fs):
参数 fs:表示评委的分数,为列表
返回值 :返回选手的得分,保留2位小数。
"""
def getScore(fs):
maxfs = 0
minfx = 999999
n = _____①_____
for f in fs:
if f > maxfs:
_____②_____
elif f < minfx:
minfx = f
yxf = sum(fs)-maxfs-minfx
avgfs = _____③ _____
return avgfs
fs = [9.56,9.68,9.78,9.67,9.81,9.21,9.75]
defen = _____④_____
print(defen)
参考程序:
def getScore(fs):
maxfs = 0
minfx = 999999
n = len(fs) - 2
for f in fs:
if f > maxfs:
maxfs = f
elif f < minfx:
minfx = f
yxf = sum(fs)-maxfs-minfx
avgfs = int(yxf / n * 100 +0.5) / 100 #或者round(yxf/n ,2)
return avgfs
fs = [9.56,9.68,9.78,9.67,9.81,9.21,9.75]
defen = getScore(fs)
print(defen)
素数判断
素数是只能被1和本身整除的正整数,编写自定义函数,实现判断正整数是否为素数。
完善程序代码。
"""
判断正整数n是否为素数,若是返回True;否则返回False
函数名 def prime(n)
参数 n:表示正整数
返回值 :n是素数,返回True;否则返回False
"""
def prime(n):
if n < 2:
return False
else:
for i in range(_____①_____ ,n):
if _____②_____ :
return False
return _____③ _____
n = 7
if _____④ _____ :
print("{}是素数".format(n))
else:
print("{}不是素数".format(n))
参考答案:
①2 ; (2分)
②n % i == 0; (2分)
③True ;(2分)
④prime(n)。(2分)
含奇数个5的个数
编写程序计算n(n<=10)位数中,包含奇数个5的个数。比如1位数中包含奇数个5的个数是1个。利用递推方法计算n位数包含奇数个5的个数。完善划线处的代码。
c = [[0 for i in range(2)] for i in range(11)] #存放奇数个5和偶数个5的二维列表
c[1][0] = 9 #一位数中包含偶数个5的个数
c[1][1] = 1 #一位数中包含奇数个5的个数
k = 9
n = 5
for i in range(2, _____①_____):
if i == n:
k = _____②_____
c[i][0] = c[i-1][1] + k * c[i-1][0]
c[i][1] = _____③ _____
print(c[n][1])
参考答案:
① n+1 ;(3分)
② k - 1 ; (3分)
③ k*c[i-1][1] + c[i-1][0] 。(4分)
快速排序
从键盘接收一组不重复整数,并将这组整数按从小到大的顺序排列。
以下程序采取快速排序法对这组整数进行排序。
快速排序法的原理是:
(1)取这组数据中间那个数为锚定值mid;
(2)从这组数据开头往右找,遇到比mid大的数则停下,位置记为i;
(3)从这组数据末尾往左找,遇到比mid小的数则停下,位置记为j;
(4)如果此时i仍在j左边,即i<=j,则交换这两个数;
(5)重复(2)~(4)直到i、j重合;
(6)对i左边的数进行快速排序;
(7)对右边的数进行快速排序。
输入示例:
请输入需要排序的一组整数,数与数之间用空格隔开:6 10 11 8 4 1 9 7
输出示例:
排序结果:1 4 6 7 8 9 10 11
程序模板:
def QuickSort(left,right):
if ______①______:
return
mid=Numbers[left+(right-left)//2]
i=left
j=right
while i<j:
while Numbers[i]<mid:
i+=1
while Numbers[j]>mid:
j-=1
if i<=j:
______②______
QuickSort(left,j-1)
QuickSort(i+1,right)
Numbers=list(map(int,input("请输入需要排序的一组整数,数与数之间用空格隔开:").______③______ ))
QuickSort(0, ______④______ )
print("排序结果:",end="")
for i in Numbers:
print(i,end=" ")
参考答案:
(1)left>=right;(2分)
(2)Numbers[i],Numbers[j]=Numbers[j],Numbers[i];(2分)
(3)split();(2分)
(4)len(Numbers)-1。(2分)
鸡兔同笼
鸡兔同笼是中国古代的数学名题之一。大约在1500年前,《孙子算经》中就记载了这个有趣的问题。书中是这样叙述的:今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?意思是:有若干只鸡兔同在一个笼子里(笼中最少有一只鸡和一只兔),从上面数,有35个头,从下面数,有94只脚。问笼中各有多少只鸡和兔?今天我们用编程的方法来求解一下这道数学命题吧。
def ji_tu(head,leg):
j=0
t=0
while j<head:
j += 1
t = ______① ______
if (leg== ______② ______):
print('有鸡{}只,有兔子{}只。'.format(______③______))
return (j,t)
while True:
try:
sum_head=int(input('请输入总头数:'))
sum_leg=int(input('请输入总脚数:'))
if ______④______:
print('输入鸡和兔子的总头数或总脚数错误,请重新输入!')
else:
ji_tu(______⑤______)
except:
print('能不能正常输入数据?')
参考答案:
(1)head-j ; (2分)
(2)(j2+t4); (3分)
(3)j,t; (2分)
(4)sum_head<2 or sum_leg<6 ; (3分)
(5)sum_head,sum_leg。 (2分)
数数游戏
有一个游戏:有两个人,第一个人先从1和2中挑一个数字,第二个人可以在对方的基础上选择加1或者加2,然后又轮到第一个人,他也可以选择加1或者加2,之后再把选择权交给对方,就这样双方交替地选择加1或者加2,谁先加到20,谁就赢了。在不考虑谁输谁赢的情况下,从一开始(以1或2为起点)加到20,有多少种不同的递加过程?比如1,3,5,9,11,13,15, 17 ,19,20算一种;2,3,5,6,8,10,11,12,14,16,18,20又是一种。那么一共会有多少种这样的过程呢?我们可以用递归算法来解决这个问题,请补全代码。
def guo_cheng(n):
if ______①______:
return n
return ______②______
# 输出所有过程的个数
print (guo_cheng( ______ ③ ______ ))
参考答案:
(1)n==1 or n==2; (3分)
(2)guo_cheng(n-1)+guo_cheng(n-2) ; (4分)
(3)20 。 (3分)
验证哥德巴赫猜想
任意一个大于等于4的偶数总可以分解为两个素数之和。请在
下面的横线上补全代码,使得通过键盘输入一个偶数x(x<1000,输出这两个素数。
如果有多组解,只需要输出一组,并且第一个素数要尽可能地小。例如,输入“10”,
输出“3 7“;输入“18”,输出“5 13”。
def prime(x):
for i in range(2, x):
if x%i == 0:
return ______① ______
return 1
x=int(input("输入一个偶数x:"))
for k in range( ______②______,x//2+1):
if prime(k) and prime(______ ③______ ):
print(______④______ )
break
参考答案:
def prime(x):
for i in range(2, x):
if x%i == 0:
return 0
return 1
x=int(input("输入一个数x:"))
for k in range(2,x//2+1):
if prime(k) and prime(x-k):
print(k,x-k)
break
分治算法判断回文数
回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数,例如12321、765567就是回文数。请补全下列代码,编程实现用分治的方法判断一个整数是否是回文数。
def ispel(s):
num = len(______①______)
if num == 0:
return False
if num == 1:
return True
if num == 2:
return s[0] ==______②______
else:
return s[0] == s[num - 1] and ispel(s[1: ______③ ______])
st = input("请输入一个整数:")
if ______④______ == True:
print("输入的是回文数")
else:
print("输入的不是回文数")
参考程序:
def ispel(s):
num = len(s)
if num == 0:
return False
if num == 1:
return True
if num == 2:
return s[0] == s[1]
else:
return s[0] == s[num - 1] and ispel(s[1:num - 1])
st = input("请输入一个整数:")
if ispel(st) == True:
print("输入的是回文数")
else:
print("输入的不是回文数")
小青蛙爬楼梯
楼梯有n级。小青蛙每次只能爬1级或2级。
当楼梯只有1级时,青蛙只有1种爬法。
当楼梯有2级时,青蛙有2种爬法:一次爬2级;一次爬1级,爬2次。
请从键盘上接收楼梯级数n,输出青蛙有几种爬法。
示例输入
请输入楼梯级数:8
示例输出
8级楼梯共有34种爬法。
程序如下:
def Climb(n):
if ______①______:
return 1
elif n==2:
______②______
else:
return ______③ ______
n=int(input("请输入楼梯级数:"))
if n>0:
print("%d级楼梯共有%d种爬法。"%(______④______,______⑤______))
参考程序:
(1)n==1; (2分)
(2)return 2; (2分)
(3)Climb(n-1)+Climb(n-2); (2分)
(4)n; (2分)
(5)Climb(n).(2分)
字符加密
将大写字母逐个按其ASCII值转换为7位二进制数,并在最左边补0,使得每个字母转换为8位二进制数,然后将8位二进制数每四位转为十六进制数。如明文是"CIE",加密后的密文是"434945"。编写的python程序如下,完善划线处的代码。
def xtob(n): #将整数转为二进制数
if n <= 1:
return str(n)
return xtob(n//2)+_____①_____
mingwen = "CIE"
he = '0123456789ABCDEF'
rst = ''
for c in mingwen:
s = "0" + xtob(ord(c)) #将明文转为8位二进制数
i = 0
data = 0
while i < 8:
data =data * 2 +_____② _____
if (i + 1) % 4 == 0:
rst = rst + he[data]
data = 0
_____③_____
print('密文是:',rst)
参考程序:
def xtob(n): #将整数转为二进制数
if n <= 1:
return str(n)
return xtob(n//2)+str(n%2)
mingwen = "CIE"
he = '0123456789ABCDEF'
rst = ''
for c in mingwen:
s = "0" + xtob(ord(c)) #将明文转为8位二进制数
i = 0
data = 0
while i < 8:
data = data * 2 + int(s[i])
if (i + 1) % 4 == 0:
rst = rst + he[data]
data = 0
i += 1
print('密文是:',rst)
说明:本题将每个大写字母转换为二进制数,①处代码是递归的方法将十进制转二进制,若整数不是0或1的时候,继续整除2,因此①处代码是xtob(n//2)+str(n%2);8位二进制数每4位二进制数转十六进制数,因此②处的代码是data * 2 + int(s[i]) ;③处的代码是循环变量i自增1,因此该处代码是i=i+1。
辗转相除法求最大公约数
辗转相除法求最大公约数,下列函数是用递归算法实现的,请完善横线处的代码。
def gcd(a,b):
m=a%b
if m==0:
return _____①_____
else:
a=b
_____②_____
return _____③_____
print(gcd(12,18))
参考答案:
(1)b; (3分)
(2)b=m;(3分)
(3)gcd(a,b)。(4分)
寻找列表中的最大值
下面的程序运用分治算法寻找列表中的最大值。请将空格补全代码。
#子问题规模小于或等于2时
def zui_da_zhi(a_list):
if _____①_____:
if a_list[0]>=a_list[1]:
most=a_list[0]
else:
most=a_list[1]
else:
most=a_list[0]
return most
# 分治算法排序
def fen_zhi(init_list):
n=len(init_list)
if n<=2: #若问题规模小于或等于2,解决
return zui_da_zhi(init_list)
#分解(子问题规模为n/2)
left_list,right_list=_____②_____
#递归,分治
left_max,right_max=_____③_____
#合并
return zui_da_zhi([left_max,right_max])
#测试数据
test_data=[12,25,4,47,69,5,4,6,37,89,21]
print('最大值为:',fen_zhi(test_data))
参考答案:
(1)len(a_list) == 2; (2分)
(2)init_list[:n//2],init_list[n//2:]; (3分)
(3)fen_zhi(left_list),fen_zhi(right_list)。 (3分)
换位密码法
换位密码法是将明文中的字符位置通过一定的规则重新排列从而得到密文的一种加密方法。某换位密码法加密方法如下:先把明文按照固定长度(4位一组)进行分组,然后对每一组的字符进行换位操作,从而得到密文。例如, 字符串"ceit",使用密钥1432进行加密时,首先将字符串以 4 个字符为一组进行分组,然后对每组的字符进行换位,第1个和第3个字符位置不变,把第2个字符和第4个字符交换位置,从而得到密文"ctie"。小张编写的程序如下,请完善划线处的代码:
def jiami(yw,key):
result = ''
for i in range(0, _____ ①_____ ,len(key)):
s1=yw[i:i+ len(key) ]
for j in range( _____ ②_____ ):
result = result + _____③ _____
return result
yw= input('请输入待加密的明文:')
key= input('请输入密钥:')
mw= _____④_____
print(mw)
运行结果如下图所示:

参考答案:
(1)len(yw);(2分)
(2)len(key);(3分)
(3)s1[int(key[j])-1];(4分)
(4)jiami(yw,key)。(3分)
裁得正方形
一张长方形的纸,长m米,宽n米(长宽均为整数),现在要把它刚好裁成一些正方形(边长是整数),有几种裁法,如果要使裁得的正方形面积最大,可以裁多少块。小明学习了递归后,编写程序如下,首先输入长方形的长和宽,计算出结果。请完善划线处的代码:
def tj(a,b):
c = 0
minn = _____①_____
if a > b:
minn = b
for i in range(1,minn+1):
if a % i == 0 and b % i == 0:
c = _____②_____
return c
def gcd(a,b):
if b == 0:
return a
return _____③_____
chang = int(input('输入长方形的长 (单位cm)'))
kuan = int(input('输入长方形的宽 (单位cm)'))
bianchang = gcd(chang,kuan)
total = _____④_____
num = tj(chang,kuan)
print('------------结果如下-------------')
print('有{}种裁法'.format(num))
print('裁得的正方形面积最大边长是{}cm,可以裁{}块'.format(bianchang,total))
运行后的结果如下图所示:

参考答案:
(1)a;(2分) (2)c + 1;(2分) (3)gcd(b,a%b);(3分) (4)(chang // bianchang) * (kuan // bianchang)或等价答案。(3分)
积分信息查询
商超采用会员制,客户的消费信息如会员号、姓名和积分如下表所示,小方的爸爸想编写一个客户信息管理系统,其中有一个功能是:输入会员号,查询该会员的积分。
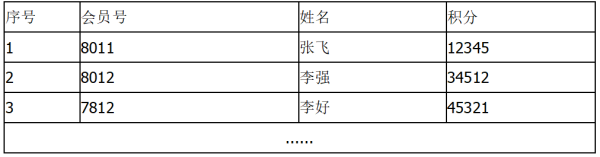
小方知道后,就跃跃欲试,他首先从数据库读取客户信息到列表data中,其中data[i][0]存储第i条记录的会员号,data[i][1]存储第i条记录的姓名,data[i][2]存储第i条记录的积分;他首先将数组data中数据按会员号升序排序,然后用二分查找算法查找会员号对应的积分信息。代码如下,完善划线处的代码:
def bubble_sort(d):
for i in range(len(d)-2):
for j in range(len(d)-1, _____①_____,-1):
if d[j][0] < d[j-1][0]:
d[j],d[j-1] = d[j-1],d[j]
def bin_ search(d, key):
i,j = 0, len(d)-1
while i <= j:
m=(i +j)//2
if _____②_____:
return m
if key > d[m][0]:
i = m+1
else:
j = m-1
return -1
#从数据库读取会员信息存列表data中,代码略
data=[[8011,'张飞',12345],[8012,'李强',34512],[7812,'李好',45321]]
bubble_sort(data)
key = int(input('输入会员号:'))
m = _____③ _____
if m!=-1:
print (data[m][1],'先生/女士:您的积分是:',data[m][2])
else:
print('该会员号不正确')
参考程序:
def bubble_sort(d):
for i in range(len(d)-2):
for j in range(len(d)-1, i,-1):
if d[j][0] < d[j-1][0]:
d[j],d[j-1] = d[j-1],d[j]
def bin_search(d, key):
i,j = 0, len(d)-1
while i <= j:
m=(i +j)//2
if d[m][0] == key:
return m
if key > d[m][0]:
i = m+1
else:
j = m-1
return -1
#从数据库读取会员信息存列表data中,代码略
data=[[8011,'张飞',12345],[8012,'李强',34512],[7812,'李好',45321]]
bubble_sort(data)
key = int(input('输入会员号:'))
m = bin_search(data,key)
if m!=-1:
print (data[m][1],'先生/女士:您的积分是:',data[m][2])
else:
print('该会员号不正确')
公式计算
已知某c的第n项计算步骤如下:
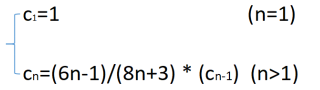
小明编写程序计算第n项的结果。首先从键盘输入n,然后利用上述递推关系计算结果,请完善划线处的代码。
def fc(n):
if n ==1:
_____①_____
else:
a=6*n-1
b=8*n+3
return _____②_____
m=int(input("请输入一个整数:"))
if not isinstance(m,int): #判断输入的m是否为整数
print('请输入一个整数')
else:
print(_____③_____)
参考程序:
def fc(n):
if n ==1:
return 1
else:
a=6*n-1
b=8*n+3
return a*fc(n-1)/b
m=int(input("请输入一个整数:"))
if not isinstance(m,int): #判断输入的m是否为整数
print('请输入一个整数')
else:
print(fc(m))
说明:本题中已知c的第n项计算公式,第1项时c的值为1,第2项可以由第1项的基础上用公式计算,程序中编写了函数fc实现计算c的结果,在函数fc中,第1项时返回1,故①处代码是return 1 ;函数fc中②处代码是计算第n的数据,由递推公式可知该处代码是a*fc(n-1)/b ,③处代码是将输入的第m项调用函数fc计算结果,故该处的代码是fc(m)。
九九乘法表
请补全下列代码,编程实现用递归的方法输出九九乘法表。
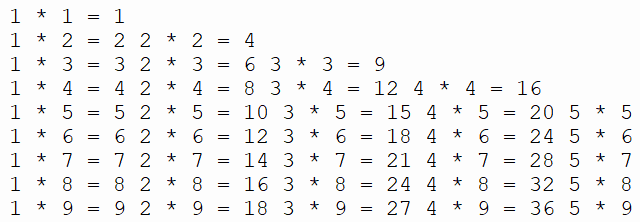
def get_result(num):
if num == 1:
print("_____①_____")
else:
get_result(_____②_____)
for i in range(1,_____③_____):
print("%d * %d = %d" % (i, num, i * num), end=" ")
print()
get_result(_____④_____)
参考程序:
def get_result(num):
if num == 1:
print("1 * 1 = 1")
else:
get_result(num - 1)
for i in range(1,num + 1):
print("%d * %d = %d" % (i, num, i * num), end=" ")
print()
get_result(9)
井底的蜗牛
有一只蜗牛在井底,井深n米。蜗牛每天往上爬a米,又会往回滑b米。
请从键盘接收输入整数n,a,b,用空格隔开。
并完成下列程序,计算蜗牛爬出这口井需要几天。
n,a,b=input("请输入井深,蜗牛每天往上爬几米,蜗牛滑下几米:")._____①_____
n,a,b= _____② _____
pos=0
i=0
while _____③_____:
_____④_____
_____⑤_____
print("第%d天,蜗牛距离井口%d米;"%(i,n-pos))
print("第%d天,蜗牛成功离开了深井!!"%(_____ ⑥_____))
参考程序:
n,a,b=input("请输入井深,蜗牛每天往上爬几米,蜗牛滑下几米:").split()
n,a,b=int(n),int(a),int(b)
pos=0
i=0
while pos+a<n:
i+=1
pos+=(a-b)
print("第%d天,蜗牛距离井口%d米;"%(i,n-pos))
print("第%d天,蜗牛成功离开了深井!!"%(i+1))