第19课 递归与递推
学习要点
(1)通过自定义函数的调用,实现递归方法。
(2)掌握由递归变递推的方法。
对标内容
理解基本算法中递归的概念,实现基本算法中的递归方法,掌握基本算法中由递归变递推的方法。
递归算法
情景导入
汉诺塔(Hanoi Tower),又称河内塔,源于印度的一个古老传说。大梵天创造世界的时候做了3根金刚石柱子,在一根柱子上从下往上按照从大到小的顺序摞着64片黄金圆盘。大梵天命人把圆盘从下往上按照从大到小的顺序重新摆放在另一根柱子上。并且规定,任何时候,在小圆盘上都不能放大圆盘,且在3根柱子之间一次只能移动一个圆盘。问应该如何操作?
思路分析
当只有1个圆盘时,直接从a-> c即可
当只有2个圆盘时,直接从a-> b,a-> c,b-> c
........
当有n(n>2)个圆盘时,我需要三大步:
第一步:先把上边的n-1个圆盘,从a移到 b
第二步:再把a上的最后一个圆盘移到c
第三步:最后再把b上的n-1个圆盘移到c即可
代码如下:
def hanoi(n, a, b, c):
if n == 1:
print(a," -> ", c )
elif n==2:
print(a," -> ", b )
print(a," -> ", c )
print(b," -> ", c )
else:
hanoi(n-1,a,c,b)
print(a," -> ", c )
hanoi(n-1,b,a,c)
return None
n=4
print('移动次数:{0}'.format(2**n-1))
hanoi(n,'A','B','C')
识点详解
递归的概念
在定义一个函数或过程时,如果出现调用自身的成分,则称为递归。
例如,使用以下程序计算 fx=1+2+3+4+5的值。
def fx(a):
if a<=1:
return 1;
else:
return a+fx(a-1)
print(fx(5))
递归是程序设计中的一种重要方法,它使许多复杂的问题变得简单,容易解决了。
就递归算法而言,并不涉及高深的数学知识,但要建立递归的概念、深入了解递归过程也不容易。
递归应用实例——阶乘计算
数学中阶乘的定义如下。
5的阶乘:5!=5×4×3×2×1
4的阶乘:4!=4 ×3×2×1
整数n的阶乘:n!=n × (n-1) × (n-2) ×...× 2 × 1
问题分析:
n! = n × (n-1)!,(例如5! =5×4!),而1! =1。求n的阶乘转化为求n-1 的阶乘,当n=3时,程序如下例所示。
def fact(n):
if n <= 1 :
return 1
else:
return n* fact (n - 1)
print(fact(3))
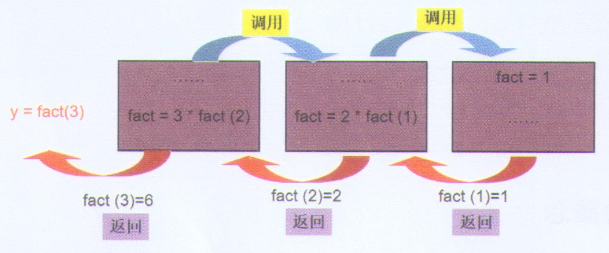
递归算法的基本思想是先把规模较大的问题变成规模较小的问题,再把规模较小的问题又变成规模更小的问题……当问题小到一定程度时,可以直接得出它的解,从而得到原来问题的解,即采用“大事化小、小事化了”的基本思想。
递归算法的实现要点
(1)递归算法有明确的结束递归的边界条件(又称终止条件)以及结束时的边界值,可以通过条件语句(if语句)实现。
(2)函数在它的函数体内调用自身(也就是找到递推关系),且向着递归的边界条件发展。
def fact(n) :
if n<=1:#边界条件
return 1
else:
return n*fact(n-1) #包含其本身*
求阶乘使用循环(递推)实现,如下例所示。
def fact(n):
s=1
for i in range(1,n+1):
s=s*i
return s
就本例而言,同学们会认为递归算法可能是多余的,费力而不讨好。但许多实际问题不可能或不容易找到显而易见的递推关系,这时递归算法就显现出了明显的优越性。
思考
(1)下列有关递归的说法,错误的是()
A. 递归算法的代码一般较少 B. 递归算法一定要有终止条件
C. 递归算法体现了“大事化小”的思想 D. 递归函数中可以不包含条件控制语句
答案:D
(2)用递归算法求1~n个连续自然数的和的程序段代码如下:
def sum(n):
if n==1:
return 1
else:
return (______)
请将代码补充完整。
答案:n+sum(n-1)
递归函数的一般写法
def f(n):
if 边界条件:
return 出口值
else:
return 递推关系
斐波那契数列指的是这样一个数列:1 、1、2、3、5、8、13、21、34......其第1项、第2项为1,从第3项开始,每一项是前两项之和。
边界条件为:f(1)=1,f(2)=1
递推关系为:f(n) = f(n-1) + f(n-2)
由以上边界条件和递推关系,可以得到如下函数:
def f(n):
if n==1 or n==2: #边界条件
return 1
else:
return f(n-1)+f(n-2) #递推关系
print(f(6))
易错点
(1)递归算法的实现要点需要识记。
(2)用分支结构描述边界条件与递归体。
模拟考题
考题1 单选题
以下函数要实现5的阶乘,则应补充的代码为()。
def function(a):
if (______):
return function(a+1)*a
else:
return 1
print(function(1))
A. a>6 B. a<6 c.="" a="">5 D. a<5
答案:B
解析∶这是要实现1×2×3×4×5的运算。
考题2 单选题
斐波那契数列∶数列从第3项开始,每一项都等于前两项之和。要计算数列第n项的值,可以使用递归函数实现,代码如下。
def fn(n):
if n==1:
return 1
elif n==2:
return 1
else:
return ______
下画线上的代码可填充下列哪个?( ) A. fn(n)+fn(n-1) B. fn(n-1)+fn(n-2) C. n+1 D. fn(n+1)+fn(n+2)
答案:B
解析∶参照斐波那契数列的定义可知,要返回前两项之和。
考题3 判断题
执行以下代码∶
ans=0
def fu(a,b,x=1):
if b==1:
return 2
global ans
ans+=fu(a-x,b-1,2)
return ans
print(fu(5,4,3))
程序输出的结果为2。( )
答案:正确
解析∶根据递归调用原理可以计算出结果。
递推算法
情景导入
递推是序列计算中的一种常用方法。它是按照一定的规律来计算序列中的每一项,通常是通过计算前面的一些项来得出序列中指定项的值,如非常有名的斐波那契数列。
你会发现大多数花朵的花瓣数目是斐波那契数列中的某一项:3,5,8,13,21 ,34 ,55,89...…例如百合花有3个花辨;梅花有5个花瓣;飞燕草有8个花瓣;向日葵不是有21个花瓣,就是有34个花辨;雏菊有34、55或89个花瓣。其他花瓣数目则很少出现。你不妨留心数数看。
知识点洋解
递归与递推的对比:
有5个人坐在一起,问第5个人多少岁,他说比第4个人大1岁;问第4个人多少岁,他说比第3个人大1岁;问第3个人多少岁,他说比第2个人大1岁;问第2个人多少岁,他说比第1个人大工岁;问第1个人多少岁,他说他8岁。请间第5个人多少岁?
以下是Python程序。
def age(n):
if n==1:
return 8
else:
return age(n-1)+1
print("第5个人"+str(age(5))+"岁")
该程序采用的是递归算法
儿童节那天,有6位同学参加了钓鱼比赛,他们每个人钓到的鱼的数量都各不相间。问第1位同学钓了多少条鱼时,他指眷第2位同学说比他多钓了2条;问第2位同学,他又说比第3位同学多钓了2条鱼……大家都说比下一位同学多钧了2条鱼。最后问到第6位同学时,他说自己钓了8条鱼。请问策1位同学钓了多少条鱼?
设第一位同学钓了k~1~条鱼,欲求k~1~,需从第6位同学的钓鱼条数k~6~入手,根据“多钓了2条鱼”这个规律,按照一定的顺序逐步进行推算。
k~6~=3 k~5~=k~6~+2=3+2=5
k~4~=k~5~+2=5+2=7
k~3~=k~4~+2=7+2=9
k~2~=k~3~+2=9+2=11
k~1~=k~2~+2=11+2=17
递推公式:k~n~=k~n+1~ + 2
初始条件:k~6~=3
通过5次计算就可求出问题答案。
本程序的递推算法可用下图来描述

递推算法程序的实现如下所示。
k=3
for i in range(1,6):
k+=2
print(k)
运行结果:
13
例题
用递推算法求斐波那契数列的前n项。
斐波那契数列指的是这样一个数列:1 、1、2、3、5、8、13、21、34......其第1项、第2项为1,从第3项开始,每一项是前两项之和。
分析:设a、b为斐波那契数列的前2项,则有a=1,b=1。
则第3项c为 c=a+b。
那第4项呢?
第4项为第2项和第3项之和。
第i项呢?
用通用公式表示为 c=a+b。
但此时的a从哪里来,b又从哪里来呢?a是上一次的b,而b是上一次的c。
python程序如下。
a=1
b=1
n=eval(input('请输入n:'))
print(a,b,end=" ")
for i in range(3,n+1):
c=a+b
a=b
b=c
print(c,end=" ")
易错点
(1)理解递归算法与递推算法的区别。
(2)能够用递归算法或递推算法解决实际问题。
模拟考题
考题1 单选题
设存一个共有n级台阶的楼梯,某入每步可走1级,也可以走2级,用递推的方式可以计算出某人从底层开始走完全部台阶的走法。例如,当n=3时,共有3种走法,即1+1+1,1+2、2+1。当n=6时,从底层开始走完全部台阶的走法共有多少种?
A. 12 b. 13 C. 14 D. 15
答案:B
解析:递推算法是一种常用算法,每次从上一次递推的结果开始,利用递推关系,求出下一次增推的结果,直到符合要求为止。通过对题目进行分析可知,由f(1)=1以及f(2)=2这两个初值以及递推关系式f(n)=f(n-1)+f(n-2)推出f(6)=13
考题2 单选题
若一个问题的求解既可以使用递归算法,也可以使用递推算法,则往往采用以下哪一种算法?
A. 递归 B. 递推 C.分治 D. 排序
答案:B
解析∶递推算法是一种常用算法,每次从上一次递推的结果开始,利用递推关系,求出下一次递推的结果,直到符合要求为止。递归算法相对递推算法要复杂得多。递归算法是递推分解问题,然后再将最简单情况的解回归成大问题的解。由于递归会引起一系列函数调用,有不少重复计算,其执行的效率也较低。因此,若某问题既能用递归算法求解,又能用递推算法求解,则使用递推方法求解更容易,效率也高得多。
递归和递推算法的比较
斐波那契数列指的是这样一个数列:1 、1、2、3、5、8、13、21、34......其第1项、第2项为1,从第3项开始,每一项是前两项之和。现在分别用递推和递归算法分别实现求斐波那契数列指定位置的值:
- 递推算法实现
def f(n):
a=1
b=1
if n<3:
return 1
else:
for i in range(n-2):
c=a+b
a=b
b=c
return c
print(f(9))
可以简化,代码如下:
def f(n):
a=b=c=1
for i in range(n-2):
c=a+b
a=b
b=c
return c
print(f(9))
- 递归算法实现
1.边界条件(出口):f(1)=f(2)=1 2.递推关系(公式):f(n)=f(n-1)+f(n-2)
def f(n):
if n<3:
return 1
else:
return f(n-1)+f(n-2)
print(f(9))
通过以上两种方式,可以发现递归算法实现比较简单易懂,递推则相对麻烦些,但递归算法有一个致命的缺陷,就是执行相率很慢,当n=50时,就需要很长时间才能出结果,而递推算法则很快。
总结:
1.递归算法简单易懂,但速度慢,对效率要求高的代码,不推荐使用
2.递推算法写起来麻烦些,但速度很快
单元测试题
模拟考题
一、单选题(共25题,每题2分,共50分)
1、下列有关循环和递归的描述正确的是?( )
A. 递归思想代码清晰简洁,可读性强
B. 递归代码中不能有循环结构的语句
C. 递归是从问题的起点出发,逐渐将复杂问题化为简单问题,最终求得问题
D. 能用递归实现的,一定能用循环代码实现
2、阅读下列程序段,数列的第6项值为多少?( )
def fibona(x):
if x==1 or x==2:
f=1
for i in range(3,x+1):
f=fibona(x-1)+fibona(x-2)
return f
n=int(input("请输入数列第几项:"))
m=fibona(n)
print("数列的第"+str(n)+"项的值为"+str(m))
A. 1
B. 8
C. 21
D. 34
3、下列程序段的运行结果为?( )
def f(n):
if n<=1:
return 1
else:
return f(n-1)*3
print(f(5))
A. 9
B. 27
C. 81
D. 243
4、对自然数1至n求和,如果将递推式f(n)=f(n-1)+n(n>1)转化成递归函数,则递归出口是?( )
A. f(1)=1
B. f(1)=0
C. f(0)=1
D. f(0)=0
5、有一对兔子,从出生后第3个月起每个月都生一对兔子,小兔子长到第三个月后每个月又生一对兔子。假如兔子都不死,要求输出一年内兔子的数量是多少。如果采用递归算法来编程,则核心的递归逻辑应该是?( )
A. f(n) =n*f(n-1)
B. f(n) = f(n-1)+n
C. f(n) = f(n-1)+f(n-2)
D. f(n) = f(n-1)+ (n-1)f(n-2)
6、下列程序使用了哪种算法?( )
def fact(n):
if n==0:
return 1
else:
return n*fact(n-1)
A. 递推
B. 递归
C. 排序
D. 分治
7、以下能正确计算出“1!+3!+5!”值(n!=1x2x3…xn)的自定义函数是?( )
A.
def f():
s=0
t=1
for i in range(1,6,2):
t=t*i
s=s+t
return s
B.
def f():
s=0
t=0
for i in range(1,6,2):
t=t*i
s=s+t
return s
C.
def f():
s=0
t=1
for i in range(1,6,2):
t=t*i
if i%2==1:
s=s+t
return s
D.
def f():
s=0
t=1
for i in range(1,6):
t=t*i
if i%2==1:
s=s+t
return s
8、下面关于递归算法的描述,错误的是?( )
A. 任何递归程序都可以改写成非递归程序
B. 定义简单,逻辑清晰
C. 算法的执行效率较高
D. 原问题与子问题在结构上必须相似
9、以下程序是用什么算法思维来显示数列 1,4,7,10,13,16 ?( )
a=1
for i in range(6):
print(a)
a+=3
A. 递归
B. 递推
C. 分治
D. 枚举
10、运行以下代码,正确的打印结果是?( )
def f():
c=0
for i in range(4,51,4):
if i%6==0:
c=c+1
return c
print(f())
A. 1
B. 2
C. 4
D. 8
11、关于递归与递推方法的比较,错误的观点是?( )
A. 递归是将复杂问题降解成若干个子问题,依次降解,求出低阶规模的解,代入高阶问题中,直至求出原问题的解;
B. 递推是构造低阶的问题,并求出解,依次推导出高阶的问题以及解,直至求出问题的解;
C. 数学上的递推关系可以通过递归的方法来实现;
D. 递归算法代码简洁,运行速度比递推快,因此应该尽量采用递归的方法;
12、下列关于递归的描述不正确的是?( )
A. 递归函数一定包含条件控制语句
B. 递归函数一定包含调用自身的语句
C. 在调用自身函数时需要明确的边界终止条件
D. 递归算法一般代码简洁,执行效率高,空间复杂度低
13、以下函数要计算x的n次方,则应补充选项为?( )
def power(x, n):
s = 1
while n > 0:
_________
s = s * x
return s
A. n = n
B. n = n+1
C. n = n-2
D. n = n-1
14、下列程序实现求菲波那契数列第4项的值:
def f(n):
if n==1 or n==2:
return 1
elif n>2:
return f(n-1)+f(n-2)
else:
return -1
print(f(4))
请问:这种解决方法属于哪种算法?( )
A. 归纳
B. 列举
C. 递推
D. 递归
15、运行下列程序,输出的结果是?( )
def f(n):
if n==1:
return 1
else:
return f(n-1)+(n-1)*f(n-1)
print(f(4))
A. 64
B. 24
C. 4
D. 16
16、编写程序计算1+1/2+1/3+……+1/n的结果,可以使用哪种调用函数自身的算法?( )
A. 枚举
B. 递归
C. 解析
D. 分治
17、用下面的程序求解计算s=1+3+5+7+9的值,请选择横线处应填写的代码?( )
def Sum(n):
if n<=1:
return 1
else:
return ________
print(Sum(9))
A. n+Sum(n-1)
B. n+Sum(n+1)
C. n+Sum(n+2)
D. n+Sum(n-2)
18、下列选项中,哪一项不是递归函数必须要具备的条件?( )
A. 明确的边界条件
B. 边界值
C. 循环语句
D. 终止条件
19、执行以下代码,程序的输出结果是?( )
def weight(n):
if n==1:
return 100
else:
return weight(n-1) +10
print(weight(3))
A. 100
B. 110
C. 120
D. 130
20、以下关于递归与递推的说法,错误的是?( )
A. 递归算法不涉及高深的数学知识,比较容易理解。
B. 递归过程一般通过函数或子过程来实现。
C. 递归算法是递推分解问题,然后再将最简单情况的解回归成大问题的解。
D. 存在既可以用递归算法解决,也可以用递推算法解决的问题。
21、一般来说,递归需要有边界条件、递归前进段和递归返回段。当不满足边界条件时,( );当满足边界条件时,( )。
A. 返回,前进
B. 中断,前进
C. 前进,返回
D. 中断,返回
22、以下哪一项不是递归算法的特征?( )
A. 要实现递归必须有一个函数,并且在这个函数体内要自己调用自己。
B. 递归必须要有判断条件,这个判断条件可以是判断次数。
C. 到达判断的条件后必须有返回,目的是结束递归。
D. 未到达判断条件时,不可以返回该函数。
23、下列程序输出正确的是?( )
def ac(n):
if n < 0:
return
else:
ac(n-1)
print(n)
ac(4)
A. 0,1,2,3,4
B. 1,2,3,4
C.
0
1
2
3
4
D.
1
2
3
4
24、运行下列程序,输出的结果是?( )
def Pell(n):
if n==1:
return 1
if n==2:
return 2
if n>=3:
return 2*Pell(n-1)+Pell(n-2)
print(Pell(4))
A. 12
B. 4
C. 3
D. 24
25、用递归算法计算10的阶乘10!的值#自定义阶乘函数。自定义函数fact(n)是求n的阶乘。
10!=1×2×3×…×10
请补全程序代码?( )
#自定义函数
def fact(n): #求阶乘
if(n==1): #终止条件
return 1 #结束递归
else: #递归条件
p=__①____ #调用递归(自身)
return p #返回乘积
#主程序
print("10!=",fact(10)) #调用递归
A. n*fact(n-1)
B. n*fact(n)
C. n*fact(n+1)
D. n**fact(n)
二、判断题(共10题,每题2分,共20分)
26、对于斐波那契数列:1,1,2,3,5,……,我们只能采用迭代公式以递推的方式求解。
正确 错误
27、递归方法的运用不仅会简化主程序的设计,也会大大减少程序的代码量。
正确 错误
28、
sum=0
for i in range(5):
sum=sum+i
print(sum)
运行以上程序,输出结果是15。
正确 错误
29、设计一个程序来求xn(x的几次方)的值,算法思想是:把xn转换为xxn-1,而xn-1又可以转换为xxn-2,如此重复下去,直到x*x0,而x0=1,从而求出了xn的值。这个程序可以用递归来实现。
正确 错误
30、函数factorialrecursive(n)与factorial cycle(n)分别是运用递归和循环计算n的阶乘的函数,因为两个函数都能够计算n的阶乘,所以递归和循环的时间复杂度是一样的。
def factorialrecursive(n):
if n == 1:
return 1
return n*factorial(n-1)
def factorial cycle(n):
result = 1
while(n>1):
result = result * n
n = n-1
return result
正确 错误
31、递归算法通常显得很简洁,因为多次调用自身,所以运行效率较高,应该大力提倡用递归算法设计程序。( )
正确 错误
32、对于递归而言,递推与回归,二者缺一不可。( )
正确 错误
33、递归算法跟递推算法是一样的,都在重复调用。( )
正确 错误
34、递推是按照一定的规律计算序列中的每一项,通常是通过计算前面的一些项来计算后一项的值。( )
正确 错误
35、一般而言,兔子在出生两个月后,就有繁殖能力,一对兔子每个月能生出一对小兔子来。如果所有兔子都不死,那么一年以后可以繁殖多少对兔子?
经分析,从第三个月起,每个月的兔子数是上个月与上上个月兔子之和。
请判读以下程序是否正确。( )
#自定义函数
def fib(n): #斐波那契数列
if n<=2:
return 1
else:
return fib(n-1)+fib(n-2) #前两个数字之和
#主程序,显示每个月兔子数(斐波那契数列)
for i in range(1,13):
print("第",i,"个月兔子对数为:",fib(i))
正确 错误
答案
一、单选题 1、A 2、B 3、C 4、A 5、C 6、B 7、D 8、C 9、B 10、C
11、D 12、D 13、D 14、D 15、B 16、B
17、D
试题解析:算式的步长为2。
18、C 19、C 20、A
21、C
试题解析:递归运行的条件,不满足边界条件前进,满足返回
22、D
试题解析:未到达判断条件时,可以返回该函数,也可以不返回
23、C
试题解析:依次输出0-4,print()默认换行
24、A 25、A
二、判断题 26、错误 27、正确 28、错误 29、正确 30、错误
31、错误
试题解析:递归算法的效率不高,并不是首选算法,应该优先选择其他效率更高的算法
32、正确
试题解析:递推关系是递归的重要组成
33、错误 34、正确
试题解析:递推是按照一定的规律计算序列中的每一项,通常是通过计算前面的一些项来计算后一项的值
35、正确