第15章 算法

学习要点

解析、枚举、排序、查找等算法。

对标内容

理解算法的概念，掌握解析、枚举、排序、查找算法的特征。能够用这些算法实现简单的Python程序。

算法与算法的表示

知识点详解

使用计算机解决问题的一般过程

使用计算机解决问题，一般分为3个阶段。

(1) 分析问题，建立模型

在解决问题前，要对问题有清晰的分析和描述。

描述的问题必须具备3个特征：

​ ①指明定义问题范畴的所有假设；

​ ②清晰地说明已知的信息；

​ ③说明何时解决问题，并根据分析情况构建数学模型。

(2 ) 设计算法

确定怎样让计算机做(用什么应用软件来解决)或让计算机怎样做(自己动手设计程序)。

(3 )实现算法及检验结果

用计算机运行设计好的算法程序解决问题，并对结果进行检测、分析和验证。

一个程序由如下两部分组成。

(1) 指令部分：指令是对计算机操作类型和操作数地址做出规定的一组符号。 指令部分由一系列的指令组成，每条指令指定了要求计算机执行的一个操作。由适当的指令构成的序列，描述了解决这个问题的计算过程。

(2) 数据部分：计算所需的原始数据、计算的中间结果或最终结果。

设计一个程序时，需要考虑以下问题。

(1) 数据的存储：计算所需要的原始数据，需要存储在不同的变量中。

(2) 计算的过程：首先必须确定解决问题的方法，接着要把该方法步骤化， 并用计算机能执行的指令来实现对应的步骤。

思考题

(1) 小杨同学在做研究性学习的课题中收集了很多数据，她想编写一个简单的计算机程序来统计、分析这些数据，则实现这一过程的一般步骤为( ）。

A. 分析问题、设计算法、编写程序、调试运行程序 B. 编写程序、分析问题、设计算法、调试运行程序 C. 编写程序、试运行程序、分析问题、设计算法 D. 设计算法、调试运行程序、编写程序、分析问题

(2 )下列是用计算机解决“计算圆周率”问题的几个步骤。

① 编制计算机程序，用计算机进行处理。 ② 分析问题，确定计算机解题任务为“计算圆周率”。 ③ 构建数学模型，设计算法。

正确的顺序是()。

A.①②③ B.③①② C.②①③ D.②③①

算法及算法的表示方法

算法的概念

算法就是对解题方法的精确而完整的描述，即解决问题的方法和步骤。除了有“计算”的问题外，日常生活中解决问题也经常要用到算法。

算法的特征

（1）有穷性：执行步骤是有限的。

（2）确定性：每个步骤的含义应是确切的。

（3）可行性：每个步骤是可行的，并且能在有限的时间内完成。

（4）有0个或多个输入：初始数据可从外界输入，也可含于算法之中。

（5）有一个或多个输出：算法一定要有结果且以一定方式输出。

算法的3种表示方法

（1）自然语言：自然语言是指人们在日常生活中使用的语言，用自然语言描述的算法通俗易懂，但缺乏直观性和简洁性，容易产生歧义。

单选题

计算圆面积的算法描述如下。

① 输入圆半径r。 ② 计算圆面积S（计算公式为S =πr^2^）。 ③ 输出结果。 ④ 结束。

上述描述算法的方法属于（）。

A.流程图 B.伪代码 C.自然语言 D.机器语言

（2）流程图：流程图也称程序框图，它是算法的一种图形化的表示方法, 与自然语言相比，它描述的算法形象、直观，更容易理解。

最常用的流程图构件有以下几种，一个完整的流程图如图15-1所示。

处理框（）:框中须指出要处理的内容，该框有一个输入和一个输出。

输入/输出框（）:用来表示数据的输入或计算结果的输出。

判断框（）：用来表示分支情况，有一个输入，一个以上输出。

连接框（）：用来连接画不下而中断的流程线。 流程线（）：用来指出流程控制方向，即动作次序。 起始框（）:用来表示程序的开始和结束。

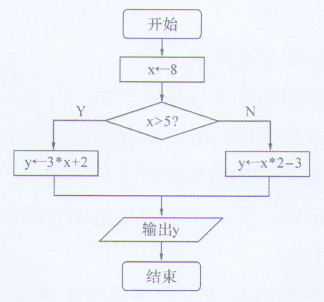
​ 图15-1 流程图

(3) 程序设计语言

算法的3种基本结构

(1) 顺序结构：在算法执行流程中，执行完一个处理步骤后，依次序执行 下一个步骤，如图15-2所示。

​ 图15-2 顺序结构

(2) 选择结构：也称分支结构或判断结构。在算法执行过程中，对某个情况e进行判断，当结果为真时，执行Y( Yes,是)指向流程线下的步骤1，否则执行N(No，否)指向流程线下的步骤2，如图15-3所示。

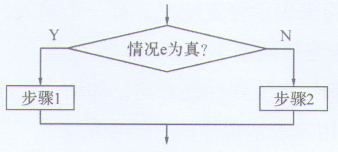
​ 图15-3 选择结构

(3)循环结构：在算法执行流程中，对某个情况e进行判断，当结果为真时，执行Y指向流程线下的步骤1；然后再次判断情况e，如果结果还为真，则再次执行步骤1,并继续判断情况e；重复上述过程，直到判断的结果为假，执行N 指向流程线下的其他语句，如图15-4所示。

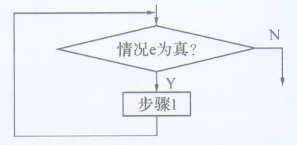
易错点

（1）在流程图中容易混淆分支结构与循环结构。

（2）经常会考算法的定义与特征，判断题容易做错。

模拟考题

考题1 单选题

以下关于算法的描述错误的是（）。

A. 算法必须要在有限的步骤内完成

B. 算法每个步骤的含义必须是确切的

C. 算法必须有输入，但可以没有输出

D. 算法可以没有输入，但必须有输出

答案：C

解析：根据算法的定义，算法必须有输出，所以选C。

考题2 判断题

使用计算机解决问题的一般过程是：设计算法、调试运行程序、编写程序、 分析问题。（）

答案：错误

解析：要理解使用计算机解决问题的一般过程，首先要分析问题，建立模型； 然后设计算法；接着实现算法（编写程序）及检验结果（调试运行程序），题目中把顺序弄错了。 

解析算法

问题引入

用基姆拉尔森公式计算某天是星期几。

W=(D+2*M+3*(M+1)//5+Y+Y//4-Y//100+Y//400+1) % 7

Y表示年，是4位数，如2022； M表示月，D表示日。

注意：(1 )该公式中要把1月和2月分别当成上一年的13月和14月处理。 例如：2022年1月4日要换成2021年13月4日代入公式。

(2)该式的运算 结果与星期几的对应关系为，0代表星期日，1代表星期一……6代表星期六。

知识点详解

1. 解析算法的概念 (1) 解析：用数学公式描述客观事物间的数量关系。

   (2) 解析算法：用解析的方法找出表示问题的前提条件与结果之间关系的数学表达式，并通过表达式的计算来实现问题的求解。

   例如：计算以速度v作匀速直线运动的一个物体，在t秒内经过的距离s, 则可通过公式s = vt得到。

2. 解析算法的程序实现 (1 ) 建立正确的数学模型(得出正确的数学计算式)。

   (2 ) 将数学表达式转换为Python表达式。

   用Python编制解析算法程序时，必须保证计算过程描述的正确性。特别是把数学表达式转换成Python表达式时，必须注意这种转换的正确性，否则容易发生运算结果错误或运行过程出错的情况。

   思考题

   (1 )计算长方体体积的算法描述如下。

   ① 输入长方体的长(z)、宽(w)、高(h)。 ② 计算长方形体积v = zwh。 ③ 输出结果。 ④ 结束。

   上述算法属于（）。

   A. 枚举算法 B.排序算法 C.解析算法 D.递归算法

   (2) 下列问题适合用解析算法求解的是（）。

   A. 将13张纸牌按从小到大进行排列 B. 统计100以内各位数字之和恰好为10的偶数的个数 C. 计算一辆车行驶100千米的油耗 D. 寻找本年级身高最高的同学

   (3) 有如下问题：

   ①已知圆锥体的半径r和高度h，使用公式V= πr^2^h求出此圆锥体的体积。 ②已知班级中每位同学的期中考试成绩总分为s，按照s的值从大到小的顺序进行成绩排名。 ③已知圆的周长s，利用公式r = s/(2π)求半径r。

   属于解析算法的选项是（）。

   A.①② B.①③ C.③④ D.②④

   （4）出租车计价规则：3千米以内，收费10元；超出3千米，每千米多收 2元。假定千米数为x，收费金额为y。解决此问题的公式和流程图如下图所示。

   

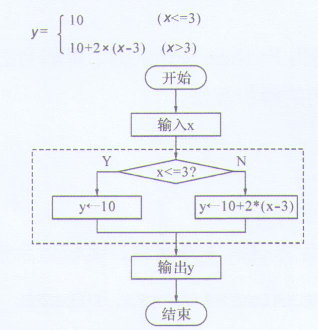
流程图加框处部分的算法属于（）。

A.解析算法 B.排序算法 C.枚举算法 D.递归算法

例题

某书店出租图书的费用标准如下：借书一天内，收费2元；借书超过一天的, 超过部分按每天0.8元收取。最后费用按四舍五入折算成整数。程序算法如下图所示。

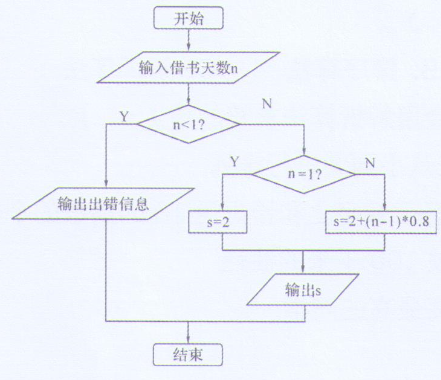
n=eval(input('输入借书天数:'))
if not n<1:
    if n==1:
        s=2
    else:
        s=2+(n-1)*0.8
    print ('费用(元)：',s)
else:
    print('输入有误！')

易错点

(1 )将数学表达式转为Python表达式时，可能会把运算符、运算顺序写错。

(2 )要留意分支结构的解析算法。

模拟考题

考题1 选择题

问题如下图所示，用计算机解决该问题，比较适合使用()。

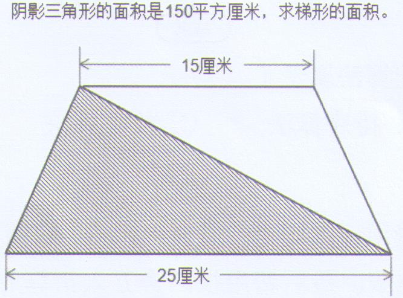
A. 排序算法 B. 枚举算法 C. 解析算法 D. 查找算法

答案：c

解析：用数学公式解决问题属于解析算法的概念。

考题2 判断题

质数是指在大于1的自然数中，除了1和它本身以外，不再有其他因数的自然数。小明想编程求出1-2000质数的个数，他应该采用解析算法。()

答案：错误

解析：不好用数学公式计算质数的个数，得用枚举算法解决问题，从1到 2000, 一个一个进行判断。

参考程序：

for n in range(1,2001):
    f=True
    for i in range(2,n): 
        if n/i==n//i:  #n%i==0
            f=False
            break
    if f :   
        print(n,'是质数。')

枚举算法

问题引入

模糊单据：一张单据上有一个5位数的编号，其百位数和十位数处已经变得 模糊不清，如图15-5所示。但是知道这个5位数是37或67的倍数。请你编写程序， 找出所有满足条件的5位数，并统计这些5位数的个数。

​ 图15-5 模糊单据

知识点详解

枚举算法的概念

枚举算法又叫穷举算法，其基本思想是把问题所有的解一一地罗列出来，并对每一个可能解进行判断，以确定这个可能解是否是问题的真正解。若是，就采纳这个解，否则就抛弃它。即使中途找到符合的解也要继续找下去，将所有可能都找完才结束。

枚举算法的程序实现

(1 ) 列举与检验过程既不重复也不遗漏。

(2 )尽可能地使可能解的罗列范围最小，以提高解决问题的效率。

(3) 用循环语句(for语句)在一定范围内列举所有可能的解。

(4) 用选择语句(if语句)判断和选择真正的解。

枚举算法的一般格式：

循环结构：
    循环体内判断：

思考题

(1 )用50元钱兑换面值为1元、2元、5元的纸币共25张。每种纸币不少于1张，问有多少种兑换方案。求解这个问题，最适合的算法是( )。

A.排序算法 B.递归算法 C.枚举算法 D.解析算法

(2)如果一个自然数恰好等于它的因子之和，这个数就称为”完全数”。例如，6就是一个“完全数”，因为6的因子为1、2、3，而6 = 1 + 2 + 3。设计一 个算法找出1000以内所有的“完全数”，那么求解这个问题主要用到的算法是 ()。

A.递归算法 B.排序算法 C.解析算法 D.枚举算法

(3)下列问题适合使用枚举算法解决的是( )。

A. 计算本月的电费 B. 计算全班男同学的平均身高 C. 查找100以内所有能被2和3整除的整数 D. 200米短跑比赛成绩排名

(4) 用枚举算法求解“找出所有满足各位数字之和等于7的三位数”时, 在下列所列举的数值范围内，算法执行效率最高的是()。

A. 0-999 B. 100-999 C. 100-700 D. 106-700

例题1

陈丽忘记了支付宝的支付密码，她急需在30分钟内完成货款的支付，请用 Python编程帮她找回密码。她零星记得自己的支付密码信息：

(1) 密码是6位数字，前面两位为85； (2) 最后两位数字相同； (3) 能被13和33整除。

参考代码

for i in range(10000):
    s=850000+i
    if s%13==0 and s%33==0:
        a=s%10
        b=s//10%10
        if a==b:
            print(s)

例题2

有一盒乒乓球，9个9个地数，最后余下7个；5个5个地数，最后余下2个；4个4个地数，最后余下1个。问这盒乒乓球至少有多少个?

参考代码1

n=16
while True:
    if n%9==7 and n%5==2 and n%4==1:
        print(n)
        break
    n+=1

参考代码2

n=16
while True:
    if n%5==2:
        break
    n=n+9
while True:
    if n%4==1:
        break
    n=n+45
print(n)

易错点

(1)要尽可能地使可能解的罗列范围最小，以提高解决问题的效率。

(2 )列举与检验过程不能遗漏。

模拟考题

考题1 编程题

明明请你帮忙寻找100~999的所有“水仙花数”，并统计个数。“水仙花数”是指各位数字的立方和等于该数本身的3位数，例如153=1 x 1 x 1 + 5 x 5 x 5 + 3 x 3 x 3。要求输出结果如下所示：

153
360
361
407

请编程实现上述功能，或补全代码。

for i in range(___①___):
    x=i
    a=x % 10 
    x= ___②___
    b=x % 10
    c=x // 10
    if （___®___）:
        print(i)

评分标准：

① 100,1000或等效答案（3分） ② x//10或等效答案（3分） ③ a*a*a* +b*b*b* +c*c*c* ==i 或等效答案（4 分）

考题2 编程题

把1296分拆成a、b、c、d四个正整数，如果a加上2，b减去2，c乘以2，d除以2，则4个结果相等。现在请你编写程序求出这4个数。

补全下面的代码。

for a in range(1,___①___):
    b =    ___②___
    for c in range(1,1296-a-b):
            d = ___®___
        if (b-2==c*2） and （a+b+c+d==___④___):
            print(a,b,c,d)

评分标准： ① 1296 （2 分） ② a+4 （3分） ③ c*4 （ 3分） ④ 1296 （2 分）

冒泡算法

知识点详解

冒泡排序的概念

冒泡排序是在一列数据中把较大（或较小）的数据逐次向右推移的一种排序技术。冒泡排序是最简单的排序方法，分为内外两层循环。外层循序代表的 是总共要跑的遍数，2个数据比较一遍。3个数据比较两遍，以此类推，〃个数 据就跑1遍。内层循环真正比较数据大小，每次比较都会将大的数据放到后 面（以升序为例）。

冒泡排序过程容易理解，每一遍加工都是将本遍最大（或最小）的数据移动 至本遍的右端位置。每个数如同水中的气泡一样，小的气泡上升，被排到最上面； 而大的气泡被依次排在下面，这样的过程我们比喻成“冒泡”。冒泡排序有多种 变式。

冒泡排序的基本思想（以升序为例）

依次比较相邻的两个数，将小数放在前面，大数放在后面。

第一遍从第1个元素开始，让它和第2个元素进行比较，若出现反序（大数 在前，小数在后）则交换；然后让第2个元素和第3个元素进行比较，若出现反序则交换；依次类推，直到比较完最后一对元素为止。第一遍排序结束时，最后 一个元素为所有元素中的最大值。

接下来进行第二遍排序。从第1个元素开始，让它和第2个元素进行比较， 若出现反序则交换；然后让第2个元素和第3个元素进行比较，若出现反序则交 换；依次类推，直到比较完最后一对元素（即倒数第二对数）为止。这样，倒数 第二个数为第二大的数。

......

n个数排序共需进行n-1遍。 

实例模拟：

冒泡程序框架(伪代码)

for i (0 ~ n-1)    #共进行n-1遍排序
    for j (0 ~ n-1-i)    # 第 i 遍排序
        if数据对反序，则：
            交换数据对

冒泡程序程序的实现(升序)

a=[1,3,2,5,8,7,6]
count = len(a)
for i in range(0, count-1):
    for j in range(0, count-1-i):
        if a[j] > a[j+1]:
            a[j], a[j+1] = a[j+1], a[j]
print(a)

运行结果：

[1, 2, 3, 5, 6, 7, 8]

若要将列表中的元素降序排序，该如何修改程序？

只需将代码：

if a[j] > a[j+1]:

修改为：

if a[j] < a[j+1]:

思考题

(1 )某书店在5所学校的流动售书量(单位为本)分别是80、125、64、 68、46。采用冒泡排序对其进行升序排序，完成第二遍时的结果是()。

(2)有一组原始数据：23、25、18、63、84、77、65、9、33、17。利用冒泡排序算法进行从小到大排序，最多需要进行( )次加工，才可以完成整个数据的排序。

A. 5 B. 6 C. 8 D. 9

易错点

(1)理解冒泡排序的算法原理。

(2)交换元素的本质就是变换索引号。

模拟考题

考题1 选择题

主持人大赛的成绩排名，可以采用的算法是（）。

A.解析算法 B.枚举算法 C.排序算法 D.查找算法

答案：C

解析：成绩排名问题符合用排序算法解决的问题特征。

考题2 编程题

在一列表中产生n (n>=10 )个50以内的数据，删除其重复数据并按照升序排序输出，同时输出删除数据个数。

例如输入：n=10 随机产生 a=[1,2,3,7,4,7,3,8,5,7] 输出：a=[1,2,3,4,5,7,8] 输出：共删除数据为3个

请编写程序实现上述功能，或补全代码。

import random
maxn = int(input("请输入要产生的数据个数：”))
___①___
for i in range(maxn):
    a.append(random.randrange(1,50,1))
print('原始数据：')
print(a)
key,n=0,maxn
while key<n:
    i=n-1
    while ___②___:
        i=i-1
    if i==key:
        key=key+l
    else:
        a.remove(___③___）
        n=n-1
for i in range(n）:
    for j in range(len(a(-1, i, -1):
        if a[j]< a[j-l]:
            a[j],a[j-l] = ___④___
print("去重后排序数据：”）
print(a）
print("共删除数据：”,___⑤___，”个"）

评分标准：

① a=[] （3 分） ② a[i]!=a[key] （ 4 分） ③ a[i] （ 3 分） ④ a[j-1],a[j] （3 分） ⑤ maxn-n （ 3 分）

选择排序

知识点详解

选择排序的概念

选择排序算法是对冒泡排序算法的改进。这种方法是在参加排序的所有元素中找出数值最小（或最大）的元素，如果它不是左侧第一个元素，就使它与左侧第一个元素中数据相互交换位置；然后在余下的元素中找出数值最小（或最大） 的元素，如果它不是左侧第二个元素，就与左侧第二个元素中的数据交换位置； 以此类推，直到所有元素成为一个有序的序列。

选择排序算法符合人们日常的排序习惯。

对于有n个元素的数列，用选择算法进行排序时，比较次数与冒泡排序算法 相同，但交换的次数比冒泡排序要少，因此它具有更高的效率。

选择排序的基本思想(以升序为例)

n个数排序共需进行1遍。

第一遍从第1个元素到第刀个元素中找出一个最小的元素，如果它不是第1 个元素，就让它和第1个元素交换位置。第一遍排序结束时，第1个元素为所有 元素中的最小值。

接下来进行第二遍排序。从第2个元素到第刀个元素中找出一个最小的元素, 如果它不是第2个元素，就让它和第2个元素交换位置。

第i遍排序开始时，设第i个位置上的数是当前最小数，用k来标记。让k位置上的数(d[k])与i后面的数(d[j])逐个比较，当找到一个比k位置上小的数(即 d[k]>d[j]),用k记录j的值(k=j) 。当j到达最后一个数时，一遍比较结束， 则左指向最小的数，即k记录的是最小数的位置。当i不等于左时，交换d[i]与d[k]]的值。

选择排序算法的算法实现

选择排序的程序同样采用双重循环嵌套来实现，外循环用来控制第几遍加工， 内循环用来控制进行排序元素的下标变化范围。每一遍加工结束，都需要用一个 变量来存储这一遍加工中所找出的最小(或最大)的数据的下标。

选择排序程序框架(伪代码)：

for i (0 ~ n-1)    #共进行n-1遍排序
    k=i
    for j (i+1 ~ n )    # 第 i 遍排序
        if找到一个比k位置上的元素的值小的元素，则：
            用k记录j的位置
    if i!=k ,则：
        交换i和k位置的数据

选择排序程序实现(升序)

a=[3,4,1,2,0,9,10]
count = len(a)
for i in range(0,count-1):
    k = i
    for j in range(i + 1, count):
        if a[k] > a[j]:
            k = j 
    if k!=i:
        a[k],a[i] = a[i],a[k]
print(a)

运行结果:

[0, 1, 2, 3, 4, 9, 10]

若要将列表中的元素以降序排序，该如何修改程序?

只需将代码：

if a[K] > a[j]:

修改为：

if a[k] < a[j]:

思考题

(1) 用选择排序算法对一组学生的身高数据进行升序排序，已知第一遍排序结束后的数据序列为166、169、177、175、172,则下列选项中可能是原始数据序列的是()。

A. 175、 177、 169、 166、 172 B. 177、 169、 166、 175、 172 C. 166、 177、 169、 175、 172 D. 166、 169 、 172、 175、 177

(2 )某校通过招投标中心采购一套多媒体教学设备，有5家单位参加竞标， 竞标价分别为18万元、17万元、23万元、15万元、16万元。若釆用选择排序算法对标价从高到低排序，需要进行数据互换的次数是()。

A. 1 B. 3 C. 4 D. 5

(3)下列关于排序的说法，错误的是()。

A. 相对而言，选择排序算法的效率比冒泡排序算法的效率高 B. 冒泡排序算法和选择排序算法都需要用到双循环结构 C. 对于刀个无序数据，不管是冒泡排序还是选择排序，都要经过n-1遍加工 D. 冒泡排序算法的程序实现一般要用到数组变量k，而选择排序则不需要

易错点

1. 对变量k的理解很重要。
2. 与冒泡排序的优劣对比。

模拟考题

考题1 单选题

现在一组初始记录无序的数据“7, 9, 3, 2, 5”使用选择排序算法，按从小到大的顺序排列，则第一轮排序的结果为（）。

A. 7, 9, 2, 3, 5 B. 2, 9, 3, 7, 5 C. 2, 7, 9, 3, 5 D. 2, 3, 5, 7, 9

答案：B

解析：本题考核对选择排序的概念与算法的理解，第一轮找出最小值2，与第一个数据7交换，其余数据位置不变。

考题2 单选题

列表 l=[9,2,8,6,3,4]，采用选择排序进行升序排序，第二遍排序之后的结果是（）。

A. [2,3,8,6,9,4] B. [2,8,6,3,4,9] C. [2,6,3,4,8,9] D. [2,3,4,6,8,9]

答案：A

解析：第一遍的结果是[2,9,8,6,3,4],第二遍的结果是[2,3,8,6,9,4]。

插入排序

知识点详解

插入排序的概念

插入排序的过程：先将待排序数列中的第1个数据看成一个有序的子数列， 然后从第2个数据起，将数据依次（从大到小或从小到大）逐个地插入这个有序 的子数列中，以此类推到最后一个数据。这很像玩扑克牌时一边抓牌一边理牌的过程，抓一张牌就把它插到应有的位置。

插入排序的基本思想

先将列表中的头两个元素按顺序排列（比如升序）。

接着，每次将一个待排序的元素，按其大小插入前面已经排好序的元素序列中，使序列依然有序，直到所有待排序元素全部插入完成。

例如待排数据为：5 3 5 2 8

第1次插入(只要将第2个元素与第1个元素比较)：

(1)先将要插入的数a[1]放入一个空的变量key；

(2 )将key与前面已经排好序的元素比较，key<a[0]成立，说明key要插到a[0]前面，将a[0]后移一个位置，放到a[1]中； (3 )将key放入a[0]中。

第2次插入(将第3个数插入前面已排好的有2个元素的序列)：

(1)先将要插入的数a[2]放入一个空的变量key；

(2 )将key与前面已经排好序的元素比较，key<a[1]不成立，说明key要插到a[1]后面，即a[2]中；

(3)将key放入a[2]中。

第3次插入(将第4个元素插入前面已排好的有3个元素的序列)：

(1 )先将要插入的数a[3]放入一个空的变量key；

(2)将key与前面已经排好序的序列比较，key<a[2]成立，说明key要插到a[2]前面，将a[2]后移一个位置，放到a [3]中；

(3 )再比较前一个数，key<a[1]成立，说明key要插到a[l]前面，将a[1] 后移一个位置，放到a[2]中；

(4 )再比较前一个数，key<a[0]成立，说明key要插到a[0]前面，将 a[0]后移一个位置，放到a[1]中；

(5 )将key放入a[0]中。

插入排序程序框架(升序)

a=[5,3,5,2,8]
count = len(a)
for i in range(1,count):
    key = a[i]
    j = i-1
    while j>=0 and a[j]>key:
        a[j+1]=a[j]
        j-=1
        a[j+1]=key
print(a)

运行结果：

[2, 3, 5, 5, 8]

以上代码也可以简化如下：

a=[5,3,5,2,8]
count = len(a)
for i in range(1,count):
    key = a[i]
    j = i-1
    while j>=0 and a[j]>key:
        a[j],a[j+1]=a[j+1],a[j] #交换a[j]和a[j+1]
        j-=1
print(a)

易错点

(1 )要理解插入排序的算法原理。

(2 )要记忆基础代码。

模拟考题

考题1 单选题 设一组初始记录关键字序列为[5,2,6,3,7]，利用插入排序算法进行升序排序，则第二次插入排序的结果为()。

A. [5,2,3,6,7] B. [2,5,3,6,7] C. [2,5,6,3,7] D. [2,3,5,6,7]

答案：C

解析：第一次插入排序的结果为[2,5,6,3,7]；第二次插入排序的结果为 [2,5,6,3,7]。

考题2 编程题 对于列表对象a=[5,3,5,2,8]；用插入排序算法进行升序排序，部分代码如下，请补全代码。

a=[5,3,5,2, 8]
___①___
for i in range(1, count): 
    key =___②___
    j = i - 1
    while j >= 0 and a[j] > key: 
        a[j + 1] = a[j]
        ___③____
        a[j+l] = key
print（a）

评分标准： ① count = len(a) （ 2 分） ② a[i] （3分） ③ j -= 1 （3 分）

顺序查找

知识点详解

顺序查找的概念

生活中，顺序查找的例子有很多，比如要从相册中从头开始翻阅查找一张已知的照片。查找算法是程序中经常用到的算法。假定要从n个元素中查找值x是否存在，最原始的方法是从头到尾依次查找，这种查找的方法就叫顺序查找。

查找是一种查询数据的技术，其目标是能以比较少的步骤或在较短时间内找到所需的对象。程序将按照查找的结果（找到或未找到）来决定接着应执行的步骤。 我们主要掌握顺序查找与对分查找算法。

顺序查找的基本思想是从第一个数据开始，按顺序逐个将数据与给定的数据 （查找键）进行比较，若某个数据和查找键相等，则查找成功，输出所查数据的位置；反之，输出未找到。

顺序查找的处理过程

假定列表a中有n个数据，查找键已经存储在变量key中。其处理过程是： 从列表a的第1个元素a[0]开始，依次判断各元素的值是否与查找键key相等， 若某个元素a[i]的值等于key，则找到了指定的数据，结束处理；若找遍了所有 的n个元素，无任何元素的值等于key，则结束处理，输出未找到信息。 

顺序查找的程序实现

在列表中查找元素26。

lst = [32, 17,56, 25, 26, 89, 65, 12] 
key = 26        #要查找的元素
b = -1            #要查找元素的索引
m= len(lst)     #列表长度
for i in range (0, m):
    if lst[i] == key:
        b = i
        break
if b == -1:    #-1代表元素未查找到
    print ("要查找的元素["+ str (key) + "]不在列表lst中。")
else:
    print ("要查找的元素["+ str (key) + "]的索引是：" + str (b))

思考题

(1)为找自己第一次上幼儿园时的照片，小张同学依次翻开自己的多本相册来逐张查找。这种查找方法为( )。

A.无序查找 B.顺序查找 C.对分查找 D.随机查找

(2)在 23、41、54、26、84、52、65、21中查找数字52,采用从后往前的顺序查找，需要查找的次数是(）。

A. 2次 B. 3次 C. 7次 D. 1次

易错点

(1)顺序查找算法与枚举算法的相似处与不同处。

(2 )顺序查找程序的实现。

模拟考题

考题1 单选题

对于n个元素，利用顺序查找算法，最坏的情况是查找( )次才结束。 A. n B. n/2 C. n^2^ D. log~2~n +1 答案：A

解析：根据顺序查找的定义，最坏的情况要查找〃次，也就是查找到最后一 个元素才找到。

对分查找

问题引入

从1~100随机取一个数字，以最少的次数猜中这个数字，应该怎么做呢如果从1开始以此往上猜，直到猜中数字，这是简单的顺序查找算法，每次猜测只能排除一个数字。如果从50开始猜，告诉你猜大了或者猜小了，这样每猜一次，都会将剩余的数字排除掉一半。不管取到哪个数字，你在7次之内都能够猜到，因为每次猜测都将排除很多数字!相比之下，第二种方法会更加省时，这种算法叫作对分查找算法，又称二分查找算法。

知识点详解

对分查找的概念

对分查找又称二分查找，是一种高效的查找方法。对分查找的前提是，被查找的数据序列是有序的（升序或降序）。

对分查找的基本思想是在有序的数列中，首先将要查找的数据与有序数列内处于中间位置的数据进行比较，如果两者相等，则查找成功；否则就根据数据的有序性，再确定该数据的范围应该在数列的前半部分还是后半部分；在新确定的缩小范围内，继续按上述方法进行查找，直到找到要查找的数据，即查找成功；如果要查找的数据不存在，即查找不成功。

对分查找的处理过程

若key为查找键，列表a存放n个已按升序排序的元素。在使用对分查找时，把查找范围[i，j]的中间位置上的数据a[m]与查找键key 进行比较，结果必然是如下3种情况之一。

（1）若key<a[m]，查找键小于中点a[m]处的数据。由a中的数据的递增性可以确定在（m，j）内不可能存在值为key的数据，必须在新的范围（i，m-1）中继续查找。

（2）若key = a[m]，找到了需要的数据。

（3）若key>a[m]，必须在新的范围（m + 1，j）中继续查找。

这样，除了出现情况（2），在通过一次比较后，新的查找范围将不超过上次查找范围的一半。

中间位置数据 a[m]的下标m的计算方法是∶m =（i+ j)//2 或 m = int(i +j/2)

对分查找的程序实现

（1）由于比较次数难以确定，所以用 while 语句来实现循环。

（2）在 while 循环体中用if语句来判断查找是否成功。

（3）若查找成功则输出查找结果，并用 break 语句结束循环。

（4）若查找不成功，则判断查找键在数组的左半区间还是右半区间，从而缩小范围，继续查找。

我们假设有一个列表lst =[12，17，23，25，26，35，47，68，76，88, 96]，要查找元素 key=25，则其对分查找的程序如下。

lst=[12,17,23,25,26,35,47,68,76,88,96]
key = 25
n = len(lst)
i,j= 0,n- 1
b =-1
while i<= j:
    m =(i+j)// 2
    if key == lst[m]:           
        b =m                #找到了要找的数，赋值给b
        break               #找到key，退出循环
    elif key > lst[m]:
        i = m+1
    else:
        j= m-1
if b ==-1:                  #-1代表元素未查找到
    print("要查找的元素["+ str(key)+"]不在列表lst中。")
else:
    print("要查找的元素["+ str(key)+ "]的索引是∶"+ str(b))

对分查找的查找次数估算

对元素规模为n的列表进行对分查找时，无论是否找到，至多进行log~2~n次查找就能得到结果；而使用顺序查找算法，在最坏的情况下（查找键在最后一个或没找到），需要进行n次查找，最好的情况是1次查找（查找键在第一个），平均查找次数是(n+1)/2

思考题

（1）下列有关查找的说法，正确的是（）

A. 顺序查找时，被查找的数据必须有序

B. 对分查找时，被查找的数据不一定有序

C. 顺序查找总能找到要查找的关键字

D. 一般情况下，对分查找的效率较高

（2）某列表有7个元素，依次为19、28、30、35、39、42、48。若采用对分查找算法在该列表中查找元素 48，需要查找的次数是（ ）。

A. 1 B. 2 C. 3 D. 4

易错点

（1）对分查找算法中查找区间的形成。

（2）对于分治思想的理解。

模拟考题

考题1 单选题

对于n 个元素，利用对分查找算法，最坏的情况是查找（）次才结束。

A. n B. n/2 C. n^2^ D. log~2~1

答案∶D

考题2 编程题

科技小组分2个小队搜集到西红柿生长的数据信息。2个小队将数据进行了从小到大排序∶a=[1，3，4，6，7，13，17，21]，b=[2，5，6，8，10，12，14，16，18]。请将这2个小队的数据进行合并，生成为一个从小到大有序的列表。

输入∶

1,3,4,6,7,13,17,21 
2,5,6,8,10,12,14,16,18

输出∶

[1,2,3,4,5,6,6,7,8,10,12,13,14,16,17,18,21]

请编写程序实现上述功能，或补全代码。

x = input()
s = x.split(',')
a=[]
for i in range(___①___):
    a.append(int(s[i]))
y = input()
s = y.___②___
b=[]
for i in range(len(s)):
    b.append(int(s[i]))
ret = []
i=j=0
while len(a)>= i + 1 and___③___:
    if a[i]<= b[j]:
        ___④___
        i += 1 
    else:
        ret.append(b[j])

        j+=1 
if len(a)>i:
    ret += a[i:]
if len(b)>j:
    ___⑤___
print(ret)

评分标准

①len(s）或等效答案（3分）

②split('，'）或等效答案（3分）

③len(b)>=j+1或等效答案（3分）

④ret.append(a[i])或等效答案（3分）

⑤ret+=b[j∶]或等效答案（4分）

算法单元测试

模拟考题

一、单选题(共25题，每题4分，共100分)

1、问题如图所示，用计算机解决该问题，比较适合使用？（ ）

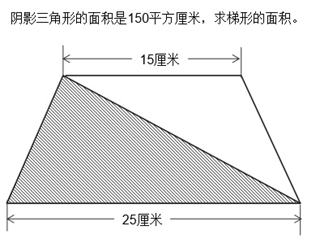   A. 解析算法

B. 枚举算法

C. 冒泡算法

D. 二分查找算法

2、现在一组初始记录无序的数据“7，9，3，2，5”使用选择排序算法，按从小到大的顺序排列，则第一轮排序的结果为？（ ）

A. 7，9，3，2，5

B. 3，2，5，7，9

C. 2，3，5，7，9

D. 2，9，3，7，5

3、关于查找的说法，下列说法正确的是？（ ）

A. 顺序查找要先对数据进行排序

B. 进行顺序查找，一定能找到数据

C. 二分查找是一种高效的查找方法

D. 二分查找法不需要对数据进行排序

4、有如下列表l=[9,2,8,6,3,4]，采用选择排序进行升序排序，请问第二趟排序之后的结果是？（ ）

A. [2,3,8,6,9,4]

B. [2,8,6,3,4,9]

C. [2,6,3,4,8,9]

D. [2,3,4,6,8,9]

5、有如下列表l=[9,2,8,6,3,4]，采用冒泡排序进行升序排序，请问第二趟排序之后的结果是？（ ）

A. [2,3,8,6,9,4]

B. [2,8,6,3,4,9]

C. [2,6,3,4,8,9]

D. [2,3,4,6,8,9]

6、有如下列表1=[10,1,9,6,3,4],采用冒泡排序进行升序排序，请问第一趟排序之后的结果是？

A. [1,3,9,6,10,4]

B. [1,9,6,3,4,10]

C. [1,6,3,4,9,10]

D. [1,3,4,6,9,10]

7、以下关于算法以及算法的描述，错误的是？（ ）

A. 算法必须要在有限的步骤内完成

B. 算法每个步骤的含义必须是确切的

C. 算法必须有输入，但可以没有输出

D. 算法可以没有输入，但必须要有输出

8、求既是3的倍数且各个位上的数的和是8的倍数的三位数，适合的算法是？（ ）

A. 解析算法

B. 枚举算法

C. 排序算法

D. 对分查找法

9、用冒泡排序算法对6个数进行排序，进行比较的次数为？（ ）

A. 4

B. 5

C. 10

D. 15

10、关于查找的说法，下列说法正确的是？（ ）

A. 顺序查找属于无序查找

B. 对分查找一定能找到数据

C. 对分查找是一种低效的查找方法

D. 顺序查找次数一定比对分查找次数多

11、某同学上完体育课回教室发现丢失了重要的物品，于是他找到班主任求助。班主任打开视频监控，然后把视频进度拖到这节课中间时间点，发现水杯已经丢了，于是判定是前半节课丢的。接着又把视频进度拖到前面一半的一半……重复以上过程，很快就锁定了物品丢失的真相。以上描述，体现出了哪一种算法思想？（ ）

A. 二分法

B. 选择排序法

C. 递归法

D. 迭代法

12、小明编写了一个插入排序的算法，为列表arr = [5, 33, 21, 67, 39, 73, 7, 43 ]中的数值进行排序，他在调试时，如下图所示有意修改了循环的次数，请问，现在代码运行后print(arr)打印出的结果是？（ ）

A. [5, 33, 21, 67, 39, 73, 7, 43]

B. [5, 21, 33, 67, 39, 43, 7, 73]

C. [5, 21, 33, 39, 67, 7, 73, 43]

D. [5, 21, 33, 67, 39, 73, 7, 43]

13、小明想对列表arr = [5, 33, 21, 67, 39, 73, 7, 43 ]中的数值进行排序，于是编写了“冒泡排序”代码，如下图。 请问，下图红线处，应该填入哪段代码？（ ）

A. arr[j] > arr[i+1]

B. arr[i] > arr[j+1]

C. arr[i] > arr[i+1]

D. arr[j] > arr[j+1]

14、对于数列3，8，11，15，17，19，25，30，44，采用“二分查找”法查找8，需要查找多少次？（ ）

A. 5

B. 4

C. 3

D. 2

15、不超过100个元素的有序数列，使用二分查找能找到指定的元素，可能的查找次数不包括？（ ）

A. 1次

B. 6次

C. 7次

D. 8次

16、猜一个2022以内的随机数，用计算机解决该问题，比较合适的算法？

A. 二分查找算法

B. 解析算法

C. 枚举算法

D. 冒泡排序算法

17、现在一组初始记录无序的数据'8,9,5,2,1',使用冒泡算法，按从小到大的顺序排列，则第三轮排序的结果为？

A. [8,5,2,1,9]

B. [2,1,5,8,9]

C. [5,2,1,8,9]

D. [1,2,8,9,5]

18、小明为了学习选择排序的算法，编写了下面的代码。针对代码中红色文字所示的一、二、三处，下面说法正确的是？（ ）

a = [8,4,11,3,9]
count = len(a)
for i in range(count-1):
    mi = i
    for j in range(i+1,count):
        if a[mi] > a[j]: #代码一
            mi = j #代码二
    if i!=mi:
        a[mi],a[i] = a[i],a[mi] #代码三
print(a)

A. 如果找到更大的元素，则记录它的索引号

B. 如果找到更小的元素，则记录它的索引号。

C. 在一趟选择排序后，不管是否找到更小的元素，mi所在元素都得与i所在的元素发生交换。

D. 代码三所在的行必然要运行。

19、在有序列表[2，3，10，15，20，25，28，29，30，35，40]中，使用二分法查找20，需要查找多少次能找到？（ ）

A. 5

B. 4

C. 3

D. 2

20、某算法的流程图如图所示，则该流程图的结构属于？（ ）

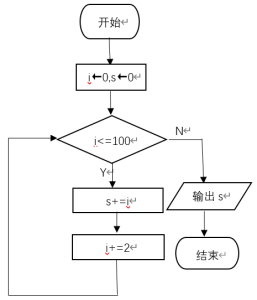
A. 顺序结构

B. 分支结构

C. 树形结构

D. 循环结构

21、“鸡兔同笼”是一个古老的数学问题，可以应用枚举法求解，也可以利用二元一次方程进行求解。以下是使用计算机解决“鸡兔同笼”问题的几个步骤： ①编写Python程序，用计算机进行处理。 ②设计“鸡兔同笼”求解算法。 ③验证算法的功能和性能。 ④分析问题，确定解题任务。 使用计算机解决“鸡兔同笼”问题，正确的步骤是？（　）

A. ②④①③

B. ④①②③

C. ④②③①

D. ④②①③

22、暴力破解是一种常见的网络攻击行为，它采用反复试错的方法去尝试破解用户的密码。这种黑客工具主要使用以下哪种算法进行设计？（　）

A. 枚举算法

B. 解析算法

C. 排序算法

D. 对分查找算法

23、对一组数据"6,1,3,2,8"进行排序，按从小到大的顺序进行排列，使用冒泡算法进行编程，则第一轮过后，排序的结果是？（　）

A. 1,6,3,2,8

B. 1,3,6,2,8

C. 1,3,2,6,8

D. 1,2,3,6,8

24、二分查找又称折半查找，下列数列中适合二分查找算法的是？（　）

A. 11 99 4 25 3 39

B. 43 71 78 81 6 55

C. 67 62 68 4 1 17

D. 85 78 59 53 19 18

25、在32枚崭新的金币中，有一枚外表与真金币完全相同的假币（质量小一点），现在只有一台天平，则应用二分法的思想最多称几次就可以发现这枚假币？（　）

A. 4

B. 5

C. 6

D. 7

答案

一、单选题

1、A 2、D 3、C

4、A

试题解析：第一趟的结果：[2,9,8,6,3,4]，第二趟的结果：[2,3,8,6,9,4]。

5、C

试题解析：第一趟的结果：[2,8,6,3,4,9]，第二趟的结果：[2,6,3,4,8,9]

6、B

试题解析：本试题考查采用冒泡排序的算法原理，根据排序的方法给出正确的答案

7、C

试题解析：算法必须要有输出。

8、B

9、D

试题解析：6个数进行冒泡排序，比较次数为5+4+3+2+1

10、A

试题解析：顺序查找和对分不一定能查找到数据。对分查找是一种高效的查找方法。如果数据元素在第一个位置，顺序查找次数不一定比对分查找次数多。

11、A

12、D

试题解析：本题考查学生对“插入排序”算法的理解，只循环了3次，所以正确答案是选项D

13、D

试题解析：本题考查学生对冒泡排序算法的理解，正确答案为选项D

14、D 15、D 16、A 17、B 18、B

19、B

试题解析：可以模拟二分法的执行过程分析得出

20、D

试题解析：算法的基本结构有顺序结构、分支结构（也叫选择结构）、循环结构。循环结构的特点是在满足某一条件的情况下，重复进行某些操作，直到条件不满足

21、D

试题解析：使用计算机解决问题的一般过程是分析问题、设计算法、编写程序、验证算法等

22、A

试题解析：解析算法是用解析的方法找出表示问题的前提条件与结果之间关系的数学表达式，并通过表达式的计算来实现问题求解。枚举算法的基本思想是把问题所有的解一一罗列出来，并对每一个可能解进行判断，以确定这个可能解是否是问题的真正解

23、C

试题解析：冒泡算法的基本思想是：两两比较相邻的数据，如果反序则交换，直到没有反序的数据为止。

24、D

试题解析：根据二分查找的实现原理,首先数列元素必须是有序的

25、B

试题解析：试题解析：二分查找法，每次都通过跟区间的中间元素对比，将待查找的区间缩小为之前的一半，直到找到要查找的元素，或者区间被缩小为 0。